Context-sensitive L-systems
(back to contents)
In the second chapter it was said that L-systems
are a variant of formal grammars. Like regular
context-sensitive grammars,
context-sensitive
L-systems try to match text on both sides
of a symbol before doing a rewrite. The difference is that matching is
more elaborate compared to regular
context-sensitive grammars.
To quote "The Algorithmic Beauty of Plants" book (text refers to
brackets in the sense of square brackets - turtle stack commands):
The introduction of context to bracketed L-systems is more difficult than
in L-systems without brackets, because the bracketed string representation
of axial trees does not preserve segment neighborhood. Consequently, the
context matching procedure may need to skip over symbols representing
branches or branch portions.
To illustrate differences let's consider an example. One of the uses of a
context-sensitive
L-system is signal propagation.
If symbol S represents a signal (for example
flower-inducing hormone) and symbol B
represents a piece of stem, then signal propogation along such
a stem could be modeled by the following
L-system:
(with-debug
(iteration-count 9)
(set-axiom (S B B B B B B B B))
(add-rule ((S < B -> S)
( B -> B)))
(add-rule (( S > B -> B)
( S -> S))))
This is how it reads:
If B has S on the left side,
then become S, else stay as B.
If S has B on the right side,
then become B, else stay as S.
This is how it rewrites:
| axiom: | (S B B B B B B B B) |
| p1: | (B S B B B B B B B) |
| p2: | (B B S B B B B B B) |
| p3: | (B B B S B B B B B) |
| p4: | (B B B B S B B B B) |
| p5: | (B B B B B S B B B) |
| p6: | (B B B B B B S B B) |
| p7: | (B B B B B B B S B) |
| p8: | (B B B B B B B B S) |
| p9: | (B B B B B B B B S) |
Now assume that the stem has branches. In that case the signal should
be propagated in all sub branches and in the main trunk as well.
The thing is that a sub branch must consider its parent branch as the
part of its left context, while the main brach must ignore sub branches
in its left context. Therefore L-system
left context is matched differenty than that in regular grammars.
For example in the word (A B [ C D [ X Y ] E [ O ]),
symbol O will consider (A B C D E) as its
left context. Notice that in the given example symbols +
and - are ignored. In fact all predefined rules except
[ and ] are ignored. To get a context matcher
to ignore user defined symbols, its rule must start with the
:nameless keyword. For example in the word
(S B B B C B B B B B), symbol C would block
signal S from propagating unless its rule is specified
in the following way (:nameless C -> C).
| axiom: |
(S B B B [ - B B B B B ] [ + B B B B B ] B B B B B) |
| p1: |
(B S B B [ - B B B B B ] [ + B B B B B ] B B B B B) |
| p2: |
(B B S B [ - B B B B B ] [ + B B B B B ] B B B B B) |
| p3: |
(B B B S [ - B B B B B ] [ + B B B B B ] B B B B B) |
| p4: |
(B B B B [ - S B B B B ] [ + S B B B B ] S B B B B) |
| p5: |
(B B B B [ - B S B B B ] [ + B S B B B ] B S B B B) |
| p6: |
(B B B B [ - B B S B B ] [ + B B S B B ] B B S B B) |
| p7: |
(B B B B [ - B B B S B ] [ + B B B S B ] B B B S B) |
| p8: |
(B B B B [ - B B B B S ] [ + B B B B S ] B B B B S) |
| p9: |
(B B B B [ - B B B B S ] [ + B B B B S ] B B B B S) |
Graphically it looks something like this:
| axiom |
p1 |
p2 |
p3 |
p4 |
p5 |
p6 |
p7 |
p8 |
p9 |
 |
 |
 |
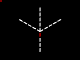 |
 |
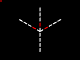 |
 |
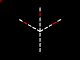 |
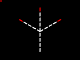 |
 |
On the other hand, the right context is matched similarly like in regular
grammars. For example the rule (A > [ B ] F -> ...) does
match A in (A [ B ] F G), but does not match
A in (A [ B C ] F G). However, there is
a small feature to skip branches in the right context. It is a special
symbol * that matches anything until the corresponding
closing square bracket. For example (A > [ B * ] F -> ...)
now matches A in (A [ B C [ D ] E ] F G).
 |
(defconstant +fibonacci+ 137.50777)
(defun segment ()
(turtle-forward 80.0))
(with-graphics
(iteration-count 7)
(add-macro (R -> roll((- +fibonacci+))))
(set-axiom (R B(:active)))
(add-option B (segment))
(add-rule ((B(x) ? (eq x :active) ->
B(:inactive) roll(+fibonacci+)
[ +(20) B(:active) ]
[ -(20) B(:active) ])
(B(x) -> B(x)))))
|
First example describes simple branching structure where each
branch splits into two sub branches.
 |
(defconstant +fibonacci+ 137.50777)
(defparameter *gravity* (create-point 0.0 -1.0 0.0))
(defun segment ()
(turtle-tropism 80.0 *gravity* 0.3))
(with-graphics
(iteration-count 7)
(add-macro (R -> roll((- +fibonacci+))))
(set-axiom (R B(:active)))
(add-option B (segment))
(add-rule ((B(x) ? (eq x :active) ->
B(:inactive) roll(+fibonacci+)
[ +(20) B(:active) ]
[ -(20) B(:active) ])
(B(x) -> B(x)))))
|
Second example introduces new turtle manipulation function
turtle-tropism.
Tropism
function takes three arguments: distance to go forward,
tropism vector and tropism strength. Tropism function is similar to
forward command in a way that it moves turtle forward,
except that turtle-tropism biases turtle movement in
a direction specified by tropism vector multiplied by tropism strength.
In this particular example tropism vector points down hence the name
*gravity*, but it can point sideways to simulate wind
tropism or upwards to simulate sun tropism.
 |
(defconstant +fibonacci+ 137.50777)
(defparameter *gravity* (create-point 0.0 -1.0 0.0))
(defun segment (s)
(turtle-set-surface s)
(turtle-tropism 80.0 *gravity* 0.3))
(with-graphics
(iteration-count 14)
(add-macro (R -> roll((- +fibonacci+))))
(set-axiom (R B(:active 1.0)))
(add-option B (segment s))
(add-rule ((B(x s) > [ B(x1 s1) * ] [ B(x2 s2) * ]
? (<= 7 *iterations-so-far*) -> B(x (+ s1 s2)))
(B(x s) ? (<= 7 *iterations-so-far*) -> B(x s))
(B(x s) ? (eq x :active) ->
B(:inactive s) roll(+fibonacci+)
[ +(20) B(:active 1.0) ]
[ -(20) B(:active 1.0) ])
(B(x s) -> B(x s)))))
|
Third example introduces context-sensitive rule.
Context-sensitive rule is used to associate
weigth with branches in such way that each "leaf" branch has the weight of 1.0,
but other branches have weight that is the sum of their children's weights.
To achieve this, B rule is divided in two parts: grow part
and propagate part. For the first half of iterations, third and fourth
B rules are used to grow the plant. For the second half of
iterations, first and second B rules are used to propagate
weights from leaves to trunk. Weights are then used with
turtle-set-surface function to set branch thickness
which is similar to radius symbol, except that it takes
branch cross section surface area as argument.
 |
(defconstant +fibonacci+ 137.50777)
(defparameter *gravity* (create-point 0.0 -1.0 0.0))
(defun segment (s)
(turtle-set-surface s)
(turtle-tropism 80.0 *gravity* (- (* 0.02 s) 0.7)))
(with-graphics
(iteration-count 14)
(add-macro (R -> roll((- +fibonacci+))))
(set-axiom (R B(:active 1.0)))
(add-option B (segment s))
(add-rule ((B(x s) > [ B(x1 s1) * ] [ B(x2 s2) * ]
? (<= 7 *iterations-so-far*) -> B(x (+ s1 s2)))
(B(x s) ? (<= 7 *iterations-so-far*) -> B(x s))
(B(x s) ? (eq x :active) ->
B(:inactive s) roll(+fibonacci+)
[ +(20) B(:active 1.0) ]
[ -(20) B(:active 1.0) ])
(B(x s) -> B(x s)))))
|
Fourth example illustrates that branch weight can be used to alter
tropism strength. "Light" branches have negative tropism strength
as if striving toward sun, while "heavy" branches have positive tropism
strength as if being bent down by gravity due to their weigth.
 |
(defconstant +fibonacci+ 137.50777)
(defparameter *gravity* (create-point 0.0 -1.0 0.0))
(defparameter *green* (create-color 0.0 1.0 0.0))
(defun segment (s)
(turtle-set-surface s)
(turtle-tropism 80.0 *gravity* (- (* 0.02 s) 0.7)))
(with-graphics
(iteration-count 14)
(add-macro (R -> roll((- +fibonacci+))))
(set-background-color (create-color 0.0 0.2 0.4))
(set-axiom (color(*green*) R B(:active 1.0)))
(add-option B (segment s))
(add-rule ((B(x s) > [ B(x1 s1) * ] [ B(x2 s2) * ]
? (<= 7 *iterations-so-far*) -> B(x (+ s1 s2)))
(B(x s) ? (<= 7 *iterations-so-far*) -> B(x s))
(B(x s) ? (eq x :active) ->
B(:inactive s) roll(+fibonacci+)
[ +(20) B(:active 1.0) ]
[ -(20) B(:active 1.0) ])
(B(x s) -> B(x s)))))
|
This and next example just add some decorations familiar
from previous chapters.
 |
(defconstant +fibonacci+ 137.50777)
(defparameter *gravity* (create-point 0.0 -1.0 0.0))
(defparameter *green* (create-color 0.0 1.0 0.0))
(defun segment (s)
(turtle-set-surface s)
(turtle-tropism 80.0 *gravity* (- (* 0.02 s) 0.7))
(when (= s 1.0) (turtle-object "blossom" 5.0)))
(with-graphics
(iteration-count 14)
(add-macro (R -> roll((- +fibonacci+))))
(set-background-color (create-color 0.0 0.2 0.4))
(set-axiom (color(*green*) R B(:active 1.0)))
(read-wavefront "blossom.obj" "blossom.png")
(read-wavefront "leaf.obj")
(add-option B (segment s))
(add-macro (L -> obj("leaf" 10.0 *green*)))
(add-rule ((B(x s) > [ B(x1 s1) * ] [ B(x2 s2) * ]
? (<= 7 *iterations-so-far*) -> B(x (+ s1 s2)))
(B(x s) ? (<= 7 *iterations-so-far*) -> B(x s))
(B(x s) ? (eq x :active) ->
B(:inactive s) roll(+fibonacci+)
[ +(20) B(:active 1.0) ]
[ -(20) B(:active 1.0) ]
[ roll((random 360)) +(60) L ])
(B(x s) -> B(x s)))))
|
(back to contents)















